[La distance la plus courte d’un point à l’autre n’est pas la ligne droite]

La distance la plus courte entre deux points est toujours une ligne droite dans la géométrie euclidienne, qui est la géométrie qui est habituellement apprise à l’école, où les figures sont bidimensionnelles et représentées sur une surface plane comme une feuille de cahier.

A la surface de la Terre, en revanche, la distance la plus courte est une courbe appelée géodésique. C’est parce que notre planète n’est pas plate ! Ainsi, c’est la géométrie riemannienne qui s’applique, tel que le font les planificateurs de vol pour tracer les itinéraires des aéronefs afin d’économiser du temps et du carburant.

Partons de Cherbourg-en-Cotentin (Latitude : 49°38′23″ Nord ; Longitude : 1°36′58″ Ouest) et choisissons une destination à même latitude: Vancouver (Latitude : 49°14′58″ Nord ; Longitude : 123°07′09″ Ouest) fait office de bonne candidate. Le trajet s’effectue sur une sphère, la Terre, dont le rayon mesure 6371 km.

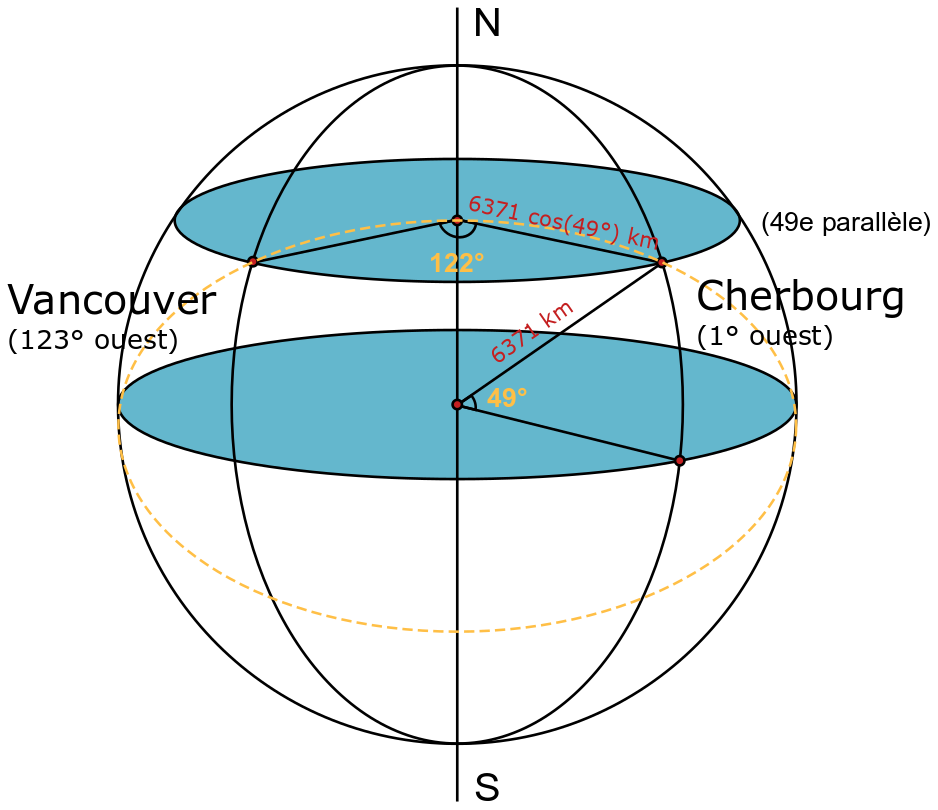
Le rayon du 49e parallèle (sur lequel se trouvent Cherbourg-en-Cotentin et Vancouver) mesure 6371 x cos(49°) = 4180 km. La distance entre Cherbourg-en-Cotentin et Vancouver en suivant cet arc de cercle est de 122/360 x 2pi x 4180 = 8900 km…

Pourquoi Google annonce-t-il alors 7731 km ?

D’abord, rassurons-nous, le chemin le plus court entre Cherbourg-en-Cotentin et Vancouver reste bien la ligne droite : un tunnel creusé entre les deux villes aurait en effet une demi-longueur de (4180 x sin(122°/2)) = 3656 km, soit 7312 km de long. L’inconvénient est qu’il serait aussi à 4344 km de profondeur où la température est estimée à plus de 4500 °C…

Reste un chemin à explorer, celui qui suit le grand cercle. Il s’agit de celui en pointillés jaunes sur la figure ci-dessus, le seul de centre commun avec la Terre et qui passe par Cherbourg-en-Cotentin et Vancouver, de même rayon par conséquent que la Terre. L’angle de cet arc de cercle est de (2 x sin^-1(3656/6371))/360 x 2pi x 6371 = 7788 km.

Au final, c’est parce que le trajet le plus court entre Cherbourg-en-Cotentin et Vancouver ne suit pas le 49e parallèle qu’il paraît si courbe, mais ce n’est qu’une illusion :

• en suivant le tunnel : 7312 km ;
• en suivant le grand cercle : 7788 km ;
• en suivant le 49e parallèle : 8900 km.

Aller plus loin:
> Géométrie différentielle : Dossier complet | Techniques de l’Ingénieur