De Charlotte Hamelin
Depuis l’Antiquité, la cryptographie (le codage d’un message pour le rendre secret) est utilisée dans les domaines parlementaires et militaires pour échanger des données sensibles sans se faire comprendre par autrui. Différentes techniques de codage sont alors apparues au fil du temps. Celles-ci ont énormément évolué à travers les époques au point où l’arrivée de la cryptanalyse (science du décodage des codes secrets) s’est révélée être un enjeu géopolitique. On peut distinguer différentes techniques de codage.
La cryptographie symétrique
Ce type de codage nécessite une clé secrète qui permet aux usagers de coder et de décoder un message en usant d’un des principes suivants :
La transposition
La transposition consiste à ne considérer la pertinence des caractères que suivant une certaine période. L’exemple de codage par transposition le plus connu est l’usage d’un scytale.

Aux IV ème et III ème siècle avant J-C, le gouvernement de Sparte était constitué de 5 magistrats appelés éphores. Pendant les nombreuses guerres qu’ils ont dû gérer, ceux-ci communiquaient avec les généraux grâce à des scytales aussi appelés bâtons de Sparte ou bâtons de Plutarque. Cette technique figure parmi les plus anciennes méthodes de cryptage de l’information connues.
Il s’agissait de bâtons de bois sur lesquels étaient enroulés des lanières de cuir. On y inscrivait alors un message en plaçant une lettre sur chaque circonvolution. Une fois la bandelette déroulée, le texte n’était plus compréhensible. Il fallait enrouler la fine lanière de cuir sur un autre scytale de même diamètre pour que le texte reprenne tout son sens. Plutarque raconte son utilisation dès 404 av J-C par Lysandre de Sparte.
La substitution monoalphabétique
Avec cette technique, à chaque fois que l’on rencontre le même caractère dans un message codé, celui-ci correspond toujours à une même lettre de l’alphabet. Pour décoder des messages utilisant ce type de substitution, la technique de cryptanalyse la plus efficace est d’effectuer une analyse des fréquences d’apparition des lettres de l’alphabet dans le message codé. En effet, toutes les lettres n’apparaissant pas avec la même régularité dans les textes écrits en Français, cela nous permet de faire des hypothèses sur les correspondances de lettres entre le message crypté et leurs déchiffrements.
Tableau des fréquences pour la langue française :
| Lettre | E | S | A | N | T | I | R | U | L | O | D | C | P |
| Pourcentage (à 0,01% près) | 17.76 | 8.23 | 7.68 | 7.61 | 7.30 | 7.23 | 6.81 | 6.05 | 5.89 | 5.34 | 3.60 | 3.32 | 3.24 |
| Lettre | M | Q | V | G | F | B | H | X | Y | J | Z | K | W |
| Pourcentage (à 0,01% près) | 2.72 | 1.34 | 1.27 | 1.10 | 1.06 | 0.80 | 0.64 | 0.54 | 0.21 | 0.19 | 0.07 | 0.00 | 0.00 |
Le chiffrement de César, le codage ROT13 ou le chiffre affine sont les techniques de cryptographie les plus connues ayant recours à la substitution monoalphabétique.
Chiffrement de César
Ce code consiste simplement en un décalage de l’alphabet. Il appartient bien à la catégorie des chiffrements monoalphabétiques puisque chaque lettre du message codé correspond toujours à une seule lettre du message décodé.
Par exemple, dans un code César+3, le A devient D etc.
| Message décodé | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| Message codé | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
Cette technique de codage a réellement été utilisée par l’empereur éponyme pendant les guerres qui l’opposaient aux tribus gauloises. Ce codage, bien qu’extrêmement simple, aurait également été exploité pendant la guerre de Sécession ainsi que par l’armée russe pendant la première guerre mondiale.
Le site dcode.fr vous propose de coder et décoder des messages secrets avec le chiffrement de César.
ROT13
Le ROT13 n’est rien d’autre qu’un code César+13. Le décalage de 13 lettres possède le grand avantage que le codage et le décodage s’effectuent de la même manière. Ce qui est un gain de temps et permet d’éviter les erreurs de chiffrement.
| A | B | C | D | E | F | G | H | I | J | K | L | M |
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
Un A sera codé en N dans le sens cryptage d’un texte. Un A sera aussi décodé en N dans le sens décryptage d’un texte.
Chiffre Affine
Pour ce code, il est nécessaire d’avoir deux clés qui constituent les coefficients d’une fonction affine. Chaque lettre de l’alphabet est associée à son rang dans l’alphabet. On calcule l’image de cette valeur par la fonction affine. Le résultat modulo 26 donne un nombre compris entre 0 et 25 qui nous donne la lettre à indiquer dans le message crypté. (attention, 0=Z, sinon 1=A ; 2=B etc…)
Exemple : On prend le chiffre affine de clé (3;4). Cela nous donne la fonction affine f définie par f(x)= 3*x+4. La lettre J est la 10ème lettre de l’alphabet. On a : f(10)=34. 34 dépasse le nombre total de lettres dans l’alphabet et 34-26=8. La 8ème lettre de l’alphabet est H donc avec cette clé de codage, la lettre J initiale sera remplacée par un H.
La substitution polyalphabétique
Contrairement à la substitution monoalphabétique, la substitution polyalphabétique consiste à un remplacement d’une lettre d’un texte « en clair » par une autre en fonction de plusieurs éléments dont la place de cette lettre à ce moment-là dans le texte. Deux « A » d’un texte ne seront donc pas nécessairement codés par un même symbole. Si on code un texte avec une clé « 1-2-3-4 », le premier caractère sera changé par la lettre suivante de l’alphabet, le second caractère par la lettre deux plus loin que celle initiale, le troisième etc. Le cinquième symbole subira le même type de modification que la 1ère lettre et ainsi de suite. Dans ces conditions, Terminus des Sciences serait codé en Uguqjpxw egv Wdkhrdgv.
D’autres codages plus poussés tels le chiffre de Vigenère ou le code Enigma utilisent la substitution polyalphabétique.
Chiffre de Vigenère
Le chiffre de Vigenère nécessite de posséder une table de Vigenère pour pouvoir coder un message, dans laquelle la lettre de la clé est en première colonne et la lettre en clair dans les 26 colonnes suivantes :
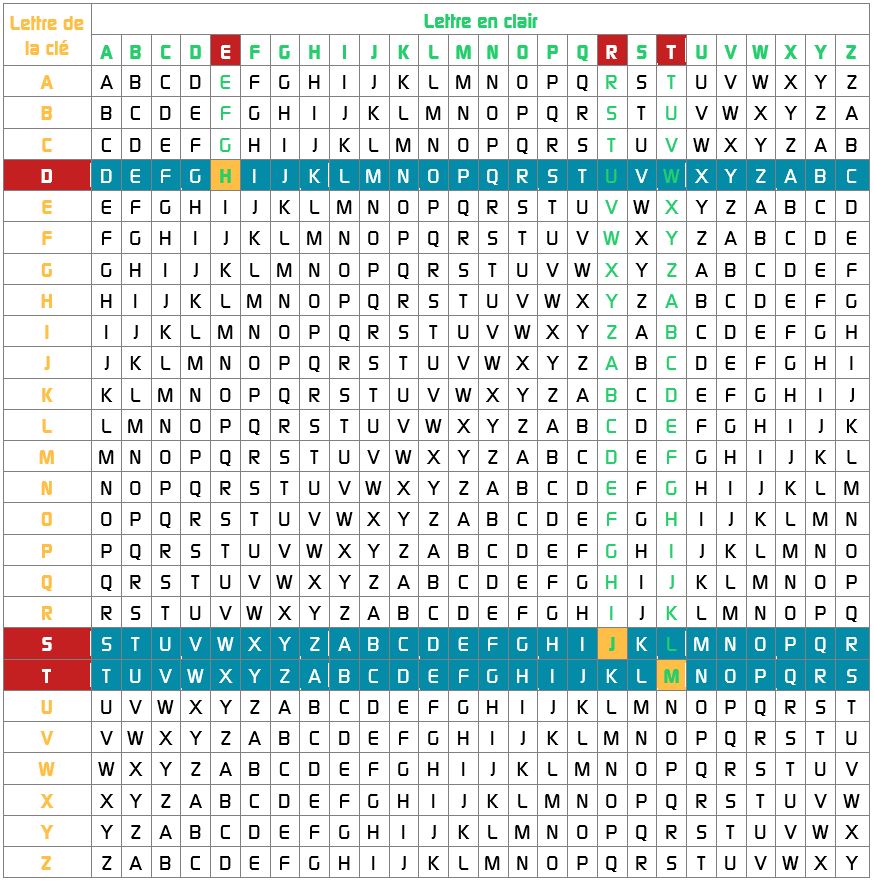
Exemple : Si notre clé est TDS alors pour crypter les mots « Terminus des Sciences », il faudra regarder dans la table ci-dessus, ce que donne le « T » du message en clair quand on l’associe au « T » de TDS, puis le « e » de « Terminus des Sciences » avec le « D » de TDS etc. Le message « Terminus des Sciences » crypté avec le chiffre de Vegenère associé à la clé TDS donne donc : « Mhjflfnv vxv kvlwgfwl ».
Enigma

La machine électromécanique Enigma, inventée par l’Allemand Arthur Scherbius à partir des travaux du Néerlandais Hugo Koch a permis aux Nazis de s’échanger des messages – rapidement et à travers toute l’Europe – qu’eux seuls étaient capables de comprendre.
Il est vite apparu aux Alliés que le décryptage du Code « Enigma » représentait une priorité majeure. La machine en elle-même est composée généralement de 5 rotors mais seuls 3 étaient sollicités à chaque nouveau réglage. La position des rotors, l’ordre de ceux-ci et le nombre de possibilités de branchement de 10 câbles entre des paires de lettres choisies parmi les 26 lettres de l’alphabet donnent près de 159.000.000.000.000.000.000 permutations différentes. Les câblages et les rotors étaient revus quotidiennement, ce qui donnait beaucoup trop de combinaisons à tester chaque jour avant de réussir à décoder le moindre message secret des Allemands.
En 1938, le gouvernement britannique, avec une aide internationale, met en place une équipe de cryptanalystes à Bletchley Park. Leur mission est d’améliorer une machine nommée « la bombe » sur laquelle ont précédemment travaillé des Polonais dont Marian Rejewski et dont le but était de tester beaucoup de combinaisons différentes en un temps court. Le plus célèbre des scientifiques ayant contribué à l’avancée de ce projet s’appelait Alan Turing. Le film – quelque peu romancé – Imitation Game retrace son histoire pendant la seconde guerre mondiale. D’autres scientifiques, dont au moins une femme, l’ont accompagné dans ses travaux de recherche. Ceux-ci sont concluants et on estime que « la bombe » de Turing aurait permis une sortie anticipée du conflit mondial de deux années. Définitivement, plus personne ne peut dire que les mathématiques ne servent à rien ! De plus, le premier ordinateur est né.
Pour comprendre son mécanisme et découvrir la face mathématique de cette machine, nous vous invitons à prendre connaissance du très bel article de Razvan Barbulescu.

Rendez-vous au musée Normandy Victory Museum près de Carentan où vous pourrez observer une des rares machines Enigma encore visibles dans le monde.
La cryptographie asymétrique
Dans les années 1970, un nouveau mécanisme de cryptage apparaît. La cryptographie asymétrique est basée sur un principe de deux clés qui sont des nombres entiers. La première est publique et permet le chiffrement. La seconde est privée et permet le déchiffrement. Ceci permet d’éviter les échanges de clés.
La cryptographie asymétrique se base sur une paire de clés créées par une personne que l’on appellera, par convention, Alice. Celle-ci porte sa clé publique à connaissance des personnes avec qui elle va interagir. Ces correspondants utiliseront cette clé pour envoyer des données chiffrées à Alice. La clé privée d’Alice lui permettra de déchiffrer ces données. La clé privée permet également à Alice de prouver son identité à ses interlocuteurs.
Etapes de la transmission d’un message d’Alice à Bob :
1. Alice écrit un message à Bob.2. Le message est chiffré à partir de la clé privée d’Alice qu’elle est seule à connaître.
3. Le message est chiffré à partir de la clé publique de Bob à laquelle Alice a accès.
4. Le message est envoyé par Alice à Bob.
5. Le message est déchiffré à partir de la clé privée de Bob qu’il est seul à connaître.
6. Authentification à partir de la clé publique d’Alice et conversion du message.
7. Bob reçoit le message « en clair »
Parmi les algorithmes de cryptographie asymétrique très utilisés, on distingue notamment le code RSA (utilisé pour le chiffrement et la signature). Cet algorithme est plus lent que ses homologues symétriques à utiliser mais permet une meilleure sécurité des informations.
Code RSA
Le chiffrement RSA, très utilisé dans le commerce électronique ou pour l’échange de données sur Internet, se base sur les travaux de Bezout ; Fermat ; Gauss ; Euclide et d’Euler dont vous pourrez trouver les détails sur cette page wikipédia . Pour créer des clés avec ce code, il faut choisir deux nombres premiers distincts. La course à la découverte de nombres premiers très grands est alors lancée.
En 1994, Peter Shor conçoit un algorithme quantique permettant de factoriser un entier naturel N même avec des diviseurs premiers extrêmement grands. Un message chiffré avec le code RSA peut être déchiffré en factorisant sa clé publique N, qui est le produit de deux nombres premiers. Cet algorithme puissant demande néanmoins de nombreux calculs qu’un simple ordinateur n’est pas en mesure d’effectuer.
L’arrivée des calculateurs quantiques change la donne et la plupart des algorithmes de cryptographie asymétrique sont maintenant vulnérables à des attaques utilisant cet appareil. Afin de garantir la sécurité en présence d’un tel adversaire, on a vu apparaître la cryptographie post-quantique.
La Cryptographie quantique et post-quantique
La cryptographie quantique vise à créer des codes utilisant des propriétés physiques plutôt que mathématiques.
La cryptographie post-quantique correspond à des techniques de codage qu’un calculateur quantique ne sera pas dans la possibilité de casser. Les principales réflexions se portent sur :
- les problèmes de vecteurs courts dans les réseaux euclidiens (1996)
- le décodage de codes linéaires aléatoires (1978)
- l’inversion de polynômes multivariés (1995)
- la navigation dans les isogénies des courbes elliptiques supersingulières (2006)
- l’inversion de fonction de hachage (1978)
Les clefs correspondant à ces algorithmes sont plus longues (jusqu’à 1000 chiffres environ) et on observe une perte d’efficacité.
A ce jour et pour longtemps, la recherche dans le domaine est un enjeu majeur pour la sécurisation de nos données.
Pour aller plus loin
Saurez-vous décoder le message caché par la Nasa sur le parachute de Perseverance ?

Pour accéder à la solution, cliquer ici.

Cryptographie et cryptanalyse de Charlotte Hamelin est mis à disposition selon les termes de la licence Creative Commons Attribution – Pas d’Utilisation Commerciale – Partage dans les Mêmes Conditions 4.0 International.
